Ce document a été proposé comme sujet de projet
informatique pour les élèves du tronc commun de
l'Ecole Polytechnique en 1998-99.
Sa difficulté est "facile" (*).
DFC - un Algorithme de Chiffrement
Auteur: Serge Vaudenay
Ecole Normale Supérieure - CNRS
1. Préambule
Afin de répondre aux besoins du commerce électronique pour faire face
à la criminalité informatique, le gouvernement américain avait
proposé un standard de chiffrement DES en 1977, mais qui est à présent
inadapté.
Un processus pour définir un nouveau standard a été lancé.
Le procédé DFC est l'un des quinze candidats à ce standard.
Cet algorithme DFC permet de chiffrer ou de déchiffrer un document
numérique au moyen d'une clef secrète.
Dans ce projet, on cherche à implémenter le procédé de chiffrement
et de déchiffrement DFC.
L'implémentation sera de préférence faite en langage Java, mais
d'autres langages pourront être envisagés.
On décrit dans un premier temps une fonction DFC qui permet de chiffrer
une chaîne arbitraire de 128 bits au moyen d'une clef représentée
par une chaîne de bits de longueur au plus 256.
2. Description de DFC
2.1. Notations
Les objets manipulés sont des chaînes de bits ou des entiers.
Les chaînes sont représentées en notation hexadécimale (lorsque
leur longueur est multiple de 4, sinon, on complète à gauche par des
zéros en précisant la véritable longueur).
Par exemple, d43x représente la chaîne 110101000011.
Les entiers sont représentés en notation décimale.
On définit les opérations suivantes.
- s
transforme la chaîne en un entier.
- l
transforme l'entier en une chaîne de longueur .
-
concaténation de deux chaînes.
- n(s)
tronque la chaîne sur ces premiers bits.
-
ou exclusif bit-à-bit de deux chaînes.
-
et bit-à-bit de deux chaînes.
-
complémentation bit-à-bit d'un chaîne.
-
opérations arithmétiques standards sur les entiers.
Par exemple, d43x=3395 et 12=d43x.
2.2. Description de Haut Niveau
La fonction de chiffrement K traite un bloc de 128 bits au moyen
d'une clef secrète de longueur arbitraire, au plus 256.
La fonction de déchiffrement K-1 opère également sur des
chaînes de 128 bits.
La clef secrète est tout d'abord transformée en une chaîne de 1024
bits ("Expanded Key") au moyen d'une fonction
("Expanding Function"), soit .
Comme cela est détaillé dans la section 2.5,
effectue un schéma de Feistel à quatre étages.
Le chiffrement lui-même est un schéma à huit étages semblable.
Chaque étage utilise une fonction ("Round Function").
Cette fonction transforme une chaîne de 64 bits en une autre au moyen
d'un paramètre de 128 bits.
Elle est décrite dans la section 2.3.
Etant donné un bloc de 128 bits , on le découpe en deux demi-blocs
de 64 bits 0 et 1 de telle sorte que 0|R1.
La clef étendue de 1024 bits est découpée en huit chaînes
de 128 bits par
où i est la -ème clef d'étage ("Round Key").
On construit alors une suite 0,...,R9 suivant la récurrence
du schéma de Feistel
i+1=RFRKi(Ri) XOR Ri-1. (i=1,...,8)
On pose alors K(PT)=R9|R8 (voir Fig. 1).
Plus généralement, à partir d'une chaîne de longueur ,
on découpe en blocs de longueur 128
La chaîne définit alors une permutation s sur l'ensemble
des chaînes de 128 bits par un schéma de Feistel à étages.
Une chaîne de 128 bits est scindée en deux parties de 64 bits
0|x1.
On construit alors la séquence 0,...,xr+1 par
i+1=RFpi(xi) XOR xi-1. (i=1,...,r)
On définit alors s(m)=xr+1|xr.
La fonction K est en fait
(qui est donc bien un schéma de Feistel à 8 étages).
La fonction est un schéma à 4 étages définit également à
partir de .
De manière triviale, on a K-1=EncrevEK où
Fig. 1: Schéma de Feistel à 8 Etages.
Pour chiffrer une chaîne de longueur arbitraire au moyen
d'une clef , on commence par coder sur 64 bits par 64 et
l'on constitue une chaîne de bits tous nuls de longueur minimale telle
que
soit de longueur multiple de 128.
On découpe alors cette chaîne en blocs de 128 bits
64)=PT1|PT2|...|PTn.
On définit ensuite la séquence 1,...,CTn par
et
i=DFCK(PTi XOR CTi-1). (i=2,...,n)
La chaîne 1|...|CTn est le résultat du chiffrement
de .
2.3. La Fonction
La fonction utilise un paramètre de 128 bits, soit deux paramètres
de 64 bits:
un "paramètre ", et un "paramètre ".
Elle traite des chaînes de 64 bits.
On définit
a|b(x)=CP(|((a.x+b)
mod(264+13))mod 264|64)
où est une permutation sur l'ensemble des chaînes de 64 bits
(que l'on définit dans la section 2.4).
Cette construction constitue un "module de décorrélation".
2.4. La Permutation
La permutation ("Confusion Permutation") utilise une table
à 6 bits d'entrée et 32 bits de sortie ("Round Table").
Si l|yr est l'entrée de où l et r sont des
chaînes de 32 bits, on définit
(yr XOR RT(trunc6(yl)))|
(yl XOR KC)+KDmod 264|64
où est une constante prédéfinie de 32 bits, et est une
constante de 64 bits.
La permutation est schématisée sur la figure 2.
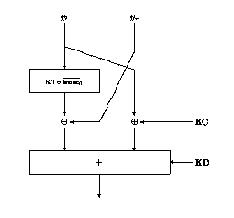
Fig. 2: La Permutation .
Les constantes , et seront définies
dans la section 2.6.
2.5. Diversification de la Clef
Afin de créer la séquence 1,RK2,...,RK8 à partir de
de longueur au plus 256, on utilise le procédé suivant.
On complète tout d'abord par une chaîne constante prédéfinie
que l'on tronque sur 256 bits pour obtenir la
chaîne ("Padded Key")
(Si est de longueur 128, on note que seuls les 128 premiers bits de
sont utiles.)
On découpe ensuite en 8 chaînes de 32 bits 1,...,PK8
telles que
1|...|PK8.
On définit
1 = PK1|PK8
OBP1 = PK5|PK4
EAP1 = PK2|PK7
EBP1 = PK6|PK3.
On définit également
i = OAP1 XOR KAi
OBPi = OBP1 XOR KBi
EAPi = EAP1 XOR KAi
EBPi = EBP1 XOR KBi
pour (où i et i sont des constantes définies dans
la section 2.6).
(Le nom des variables vient de "Odd -Parameter",
"Odd -Parameter", "Even -Parameter", et
"Even -Parameter".)
On définit
1(K)=OAP1|OBP1|...|OAP4|OBP4.
Cela définit une permutation EF1(K).
De même,
2(K)=EAP1|EBP1|...|EAP4|EBP4
définit une autre permutation EF2(K).
EF1(K) et EF2(K) permettent de définir .
On pose 0=|0|128 et
i = EncEF1(K)(RKi-1) si i est impair
EncEF2(K)(RKi-1) si i est pair.
On définit enfin
2.6. Définition des Constantes
L'algorithme utilise plusieurs constantes prédéfinies:
- 64 constantes 6),...,RT(|63|6) de 32 bits,
- une constante de 64 bits,
- une constante de 32 bits,
- trois constantes 2,KA3,KA4 de 64 bits,
- trois constantes 2,KB3,KB4 de 64 bits,
- une constante de 256 bits.
Afin de convaincre qu'aucune trappe n'a été dissimulée dans la
conception de DFC, on définit ces constantes à partir de la constante
mathématique
b7e15162 8aed2a6a bf7158x...
/___ n!
n=0
Si (" Expansion String") est l'expansion hexadécimale
des 2144 premiers bits de , on définit
et
640(EES)=KA2|KA3|KA4|KB2|KB3|KB4|KS.
La chaîne est la suivante.
b7e15162 8aed2a6a bf715880 9cf4f3c7 62e7160f 38b4da56x
a784d904 5190cfef 324e7738 926cfbe5 f4bf8d8d 8c31d763x
da06c80a bb1185eb 4f7c7b57 57f59584 90cfd47d 7c19bb42x
158d9554 f7b46bce d55c4d79 fd5f24d6 613c31c3 839a2ddfx
8a9a276b cfbfa1c8 77c56284 dab79cd4 c2b3293d 20e9e5eax
f02ac60a cc93ed87 4422a52e cb238fee e5ab6add 835fd1a0x
753d0a8f 78e537d2 b95bb79d 8dcaec64 2c1e9f23 b829b5c2x
780bf387 37df8bb3 00d01334 a0d0bd86 45cbfa73 a6160ffex
393c48cb bbca060f 0ff8ec6d 31beb5cc eed7f2f0 bb088017x
163bc60d f45a0ecb 1bcd289b 06cbbfea 21ad08e1 847f3f73x
78d56ced 94640d6e f0d3d37b e67008e1 86d1bf27 5b9b241dx
eb64749ax
On peut recalculer cette chaîne à l'aide du programme Maple par la
commande suivante.
convert(floor(evalf((E-2)*22144,800)),hex);
2.7. Un Exemple de Chiffrement
Voici un exemple de calcul qui utilise la clef
01234567890123456789012345678901x
et le message
On note ij la valeur obtenue après le tour dans le calcul de
i.
On a
01234567890123456789012345678901x
PK = 0123456789012345 6789012345678901
da06c80abb1185eb 4f7c7b5757f59584x
OAP1 = 0123456757f59584x
OBP1 = da06c80a45678901x
EAP1 = 890123454f7c7b57x
EBP1 = bb1185eb67890123x
RV10 = 0000000000000000x
RV11 = 0000000000000000x
RV12 = da2e0e338cfde0adx
RV13 = 4d94f3e1f9f88702x
RV14 = 1db16891b4d94189x
RV15 = 496d91990be5df5cx
RK1 = 496d91990be5df5c 1db16891b4d94189x
RV20 = 496d91990be5df5cx
RV21 = 1db16891b4d94189x
RV22 = a602d54d6849a8e6x
RV23 = 47fe744df4775602x
RV24 = e6965e1e1aa22ad8x
RV25 = fe338d5835695c9ex
RK2 = fe338d5835695c9e e6965e1e1aa22ad8x
RV30 = fe338d5835695c9ex
RV31 = e6965e1e1aa22ad8x
RV32 = bca2e2649c823328x
RV33 = 4e2acbfa4d334a8cx
RV34 = 3a2e390cdb84b6ffx
RV35 = 736ccee6099b8943x
RK3 = 736ccee6099b8943 3a2e390cdb84b6ffx
RV40 = 736ccee6099b8943x
RV41 = 3a2e390cdb84b6ffx
RV42 = 50203bac2471862ex
RV43 = 5efe5d55c859d94fx
RV44 = c0267e81d0868d26x
RV45 = 979d063435bd234bx
RK4 = 979d063435bd234b c0267e81d0868d26x
RV50 = 979d063435bd234bx
RV51 = c0267e81d0868d26x
RV52 = 731d89866c9df5acx
RV53 = 84c6b187fb68a1e4x
RV54 = a95a41963c2fdb84x
RV55 = b9ccb771164dfc63x
RK5 = b9ccb771164dfc63 a95a41963c2fdb84x
RV60 = b9ccb771164dfc63x
RV61 = a95a41963c2fdb84x
RV62 = 0b54cb25e107c2abx
RV63 = b5636ce10fd014a4x
RV64 = 81fa21815c0ad0aex
RV65 = 73996b00d23b5b92x
RK6 = 73996b00d23b5b92 81fa21815c0ad0aex
RV70 = 73996b00d23b5b92x
RV71 = 81fa21815c0ad0aex
RV72 = 4c3b7db300977c2fx
RV73 = 7be02f9bc16f843ex
RV74 = c339e4ae2d7e16dfx
RV75 = 13af53a7896725f2x
RK7 = 13af53a7896725f2 c339e4ae2d7e16dfx
RV80 = 13af53a7896725f2x
RV81 = c339e4ae2d7e16dfx
RV82 = c50e7eccb65c17a2x
RV83 = c9d975f72afdef6ax
RV84 = 37b2f77af0751899x
RV85 = dac0f37721ffcefax
RK8 = dac0f37721ffcefa 37b2f77af0751899x
PT = 0000000000000000 0000000000000000x
R0 = 0000000000000000x
R1 = 0000000000000000x
R2 = 6c1b4d8e52704028x
R3 = 16f3bd886ae0475bx
R4 = 393b9f7d70f861d0x
R5 = 32fb659039ed7de6x
R6 = 421352800fce6ba0x
R7 = a6d043236393c24ex
R8 = f567576616077eefx
R9 = bb46bb6ac0093c1dx
CT = bb46bb6ac0093c1d f567576616077eefx
3. Travail Demandé
Développer une application qui permet de chiffrer et de déchiffrer un
fichier.
Estimer la vitesse de chiffrement obtenu.
Quel est le coût d'une recherche exhaustive de la clef?
4. Références
- Data Encryption Standard.
Federal Information Processing Standard Publication 46,
U. S. National Bureau of Standards, 1977.
- E. Biham, A. Shamir.
Differential Cryptanalysis of the Data Encryption Standard,
Springer-Verlag, 1993.
- H. Feistel.
Cryptography and Computer Privacy.
Scientific American, vol. 228, pp. 15-23, 1973.
- M. Matsui.
The First Experimental Cryptanalysis of the Data Encryption Standard.
In Advances in Cryptology CRYPTO'94, Santa Barbara, Californie,
U.S.A., Lectures Notes in Computer Science 839, pp. 1-11, Springer-Verlag,
1994.
- S. Vaudenay.
Provable
Security for Block Ciphers by Decorrelation.
In STACS 98, Paris, France, Lectures Notes in Computer Science 1373,
pp. 249-275, Springer-Verlag, 1998.
- S. Vaudenay.
The
Decorrelation Technique Home-Page.
URL:http://lasec.epfl.ch/decorrelation.shtml